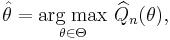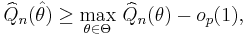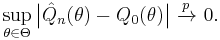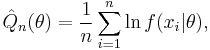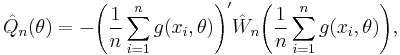Extremum estimator

In statistics and econometrics, extremum estimators is a wide class of estimators for parametric models that are calculated through maximization (or minimization) of a certain objective function, which depends on the data. The general theory of extremum estimators was developed by Amemiya (1985).

1 Definition
2 Consistency
3 Asymptotic normality
4 Examples
5 See also
6 Notes
7 References

Definition

An estimator 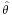$\scriptstyle\hat\theta$ is called an extremum estimator, if there is an objective function 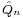$\scriptstyle\hat{Q}_n$ such that

$\hat\theta = \underset{\theta\in\Theta}{\operatorname{arg\;max}}\ \widehat{Q}_n(\theta),$

where Θ is the possible range of parameter values. Sometimes a slightly weaker definition is given:

$\widehat Q_n(\hat\theta) \geq \max_{\theta\in\Theta}\,\widehat Q_n(\theta) - o_p(1),$

where o_p(1) is the variable converging in probability to zero. With this modification 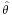$\scriptstyle\hat\theta$ doesn’t have to be the exact maximizer of the objective function, just be sufficiently close to it.

The theory of extremum estimators does not specify what the objective function should be. There are various types of objective functions suitable for different models, and this framework allows us to analyse the theoretical properties of such estimators from a unified perspective. The theory only specifies the properties that the objective function has to possess, and when one selects a particular objective function, he or she only has to verify that those properties are satisfied.

Consistency

If the set Θ is compact and there is a limiting function Q₀(θ) such that: 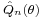$\scriptstyle\hat{Q}_n(\theta)$ converges to Q₀(θ) in probability uniformly over Θ, and the function Q₀(θ) is continuous and has a unique maximum at θ = θ₀. If these conditions are satisfied then 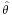$\scriptstyle\hat\theta$ is consistent for θ₀.^[1]

The uniform convergence in probability of 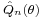$\scriptstyle\hat{Q}_n(\theta)$ means that

$\sup_{\theta\in\Theta} \big| \hat{Q}_n(\theta) - Q_0(\theta) \big| \ \xrightarrow{p}\ 0.$

The requirement for Θ to be compact can be replaced with a weaker assumption that the maximum of Q₀ was well-separated, that is there should not exist any points θ that are distant from θ₀ but such that Q₀(θ) were close to Q₀(θ₀). Formally, it means that for any sequence {θ_i} such that Q₀(θ_i) → Q₀(θ₀), it should be true that θ_i → θ₀.

Asymptotic normality

Examples

Maximum likelihood estimator uses the objective function

$\hat{Q}_n(\theta) = \frac1n \sum_{i=1}^n \ln f(x_i|\theta),$

where f(·|θ) is the density function of the distribution from where the observations are drawn.
Generalized method of moments estimator is defined through the objective function

$\hat{Q}_n(\theta) = - \Bigg(\frac1n\sum_{i=1}^n g(x_i,\theta)\Bigg)' \hat{W}_n \Bigg(\frac1n\sum_{i=1}^n g(x_i,\theta)\Bigg),$

where g(·|θ) is the moment condition of the model.
Minimum distance estimator
m-estimators

Notes

^ Newey & McFadden (1994), Theorem 2.1

References

Amemiya, Takeshi (1985). Advanced econometrics. Harvard University Press. ISBN 0-674-00560-0.
Newey, Whitney K.; McFadden, Daniel (1994). Large sample estimation and hypothesis testing. Handbook of econometrics, vol.IV, Ch.36. Elsevier Science. pp. 2111–2245. ISBN 0444887660.